Das Universum aus Information
|
|
Ist das Universum ein Computer?
|
|
|
|
|
|
|
(Entropie) In der Physik lässt sich der Informationsbegriff ("Wissen") mit dem '2. Hauptsatz der Thermodynamik' beschreiben, der aus der Wärmelehre kommt und sinngemäß lautet: Alles strebt auf einen Zustand niedrigerer Energie und damit einhergehender größtmöglicher Unordnung zu. Landläufig wird diese "Unordnung" mit Chaos gleichgesetzt, was aber so nicht stimmt.
Da man sich jedes klassische physikalische System als aus Teilchen zusammengesetzt vorstellen kann, war es naheliegend, diese mittels der Bewegungsgesetze zu beschreiben und der Gesamtheit der dabei ermittelten Information einen Wert zuzuweisen.
Da man hierbei nicht unendlich genau bei der Abzählung von Teilchen (ihrer Masse, ihrer inneren Zustände und der jeweiligen Bewegungsrichtung) vorgehen kann, bleibt ein nicht ermittelbarer Rest übrig - das Maß der Unordnung: die Entropie.
Das Bit ...ist der elementare Träger der Information. Es repräsentiert in der klassischen Welt zwei fehlerlos unterscheidbare Zustände, die jedoch an ein "Bühne" (= materiellen Träger) gebunden sind: 0 oder 1 = 1 Bit 2-dimensionale Information Jede Art von klassicher Information (Zahlen, Formeln, Programme, etc.) lässt sich in Form von Bits codieren.
|
|
|
|
|
|
|
|
|
|
Sierpinski Dreieck - ein "Chaos-Spiel" Mit dem Aufkommen der Quantenphysik musste jedoch nicht nur der Informationsbegriff erheblich erweitert werden, sondern auch das dazugehörige Verständnis.
Ähnlich wie ein (2-dimensionales) Möbiusband (R2)sich im Raum (R3) aufwölbt,
wenn man es glattzustreichen versucht, kann man sich ein Quantensystem als "Möbiuskugel" (eine sogen. "Kleinsche Flasche") vorstellen, deren Innen- und Außenoberfläche sich dabei in der 4. Dimension dreht.
(der 'blaue Punkt' ist der "Finger des Beobachters", der ununterbrochen auf der Oberfläche der Kugel bleibt, - der uns aber hier vorerst nicht weiter interessiert) Schematisch lässt sich das dann auch so darstellen:
Dieser 4-dimensionale Tetraeder ist analog einer "4-seitigen Münze", bei der jeweils zwei Eigenschaften eine Dritte bilden: Eine Bühne für die "zwei Seiten einer Medaille"
1 und 0 bilden die Bühne für die Farben rot oder grün
rot und grün bilden die Bühne für die Werte 1 oder 0
Superposition Qubit: Werte unbestimmt Jede der komplexen Zahlen a + b lässt sich jedoch wiederum im gleichen Quanten-Binärcode codieren, so dass auf jeder Ebene - rekursiv skalierbar - wieder ein Qubit mit der bereits bekannten Eigenschaft erscheint.
|
|
|
|
|
|
|
|
|
|
Wieviel Information steckt im Universum? Schichtenstruktur eines Quantensystems Die 4 möglichen verschiedenen Zustände die ein Qubit annehmen kann, setzen sich wiederum selbst aus einer Unmenge von möglichen Werten (Qubits) zusammen, die alle in Abhängigkeit zueinander stehen (... determiniert sind). Somit hat ein Quantensystem durch und durch ganzheitliche (henadische) Eigenschaften.
Wie viele Werte sind das? Diese Frage hat sich z.B.
Prof. Thomas
Görnitz gestellt und er kommt mittels
folgender Überlegung auf die Zahl von
Die Entropie eines schwarzen Loches Schwarze Löcher sind die größten Ansammlungen von Entropie im Universum, die wir kennen. Alles was hineinfällt, ist für immer verloren und kann nicht näher untersucht werden. Jedes schwarze Loch ist jedoch über (nur) 3 Eigenschaften definiert:
Es sind exakt die gleichen Eigenschaften, die auch für die Entropieermittlung in einem klassisches System aus abzählbaren Einzelteilen gelten. Betrachtet man nur ganz einfache schwarze Löcher, die keinen Drehimpuls haben und keine elektrische Ladung besitzen, findet man, dass die ... Entropie (S) sich proportional zum Quadrat ihrer Masse (Msl) verhält!
schwarze Löcher: die größte denkbare Ansammlung von Entropie Diese quadratische Abhängigkeit von der Masse hat zur Folge, dass eine noch so kleine Massenänderung zu einer linearen Änderung der Entropie führt, die proportional zur Masse des schwarzen Loches ist. Fällt ein Objekt in ein schwarzes
Loch, ist es für den Außenraum für immer verloren. Der
Entropiezuwachs des sL bei diesem Vorgang zeigt somit an, welches
Maß an Information dem Außenraum verloren geht. (
Das kleinst mögliche denkbare Objekt
wäre nun selbst ein "Mini-Black-Hole", mit dem Durchmesser einer
'Plancklänge' (ca. -
(die abstrakte, nichtlokale Quanteninformation) Setzt man nun die verschiedenen
Größen in Bezug zu Werten der Planck-Skala (kleinst
mögliche physikalische Einheiten, die auch theoretisch nicht mehr
unterscheidbar sind), lässt sich berechnen, dass dieses
"Universum" eine Entropie von etwa
Quanten-Information: Codiert auf dem Ereignishorizont eines schwarzen Loches, als auch in jedem Photon Liesse man nun das "letzte freie Photon" in dieses ultimative schwarze Loch fallen, würde man anhand des dann erfolgten Entropiezuwachses feststellen können, wie viel ein einziges Photon an unbekannter Information enthält. Und das lässt sich wiederum berechnen:
Es sind mindestens
Wie soll man sich diese ungeheure Informationsmenge, mit der wir in Form von Photonen jede Millisekunde konfrontiert werden, - vorstellen können? Das ist relativ einfach: Das physikalische Äquivalent, hat wahrscheinlich jeder schon einmal gesehen: - Es ist ein Hologramm!
.... die gleichmäßig auf einer holografischen "Fotoplatte" verteilt sind
näheres dazu: das Multiversum als Hologram |
|
|
|
|
|
|
|
|
|
- eine Grundeigenschaft der Natur -
Obwohl Quantensysteme sich scheinbar ständig auf sich selbst falten, lassen sich Unterschiede in den einzelnen Schichten zeigen, die - wie weiter oben beschrieben - äußerlich (im 'Ganzen') nicht erkennbar sind, aber sich bei einem Messprozess (= in Beziehung Setzung) sich als Interferenzen zeigen
Da Quantenphysik die 'Physik der Beziehungen' ist, müssen wir uns nun damit beschäftigen, wie diese überaus vielfältigen Beziehungen in Form von Quantensystemen "in's Sein" kommen, damit wir sie 'greifen' können und nicht nur darüber philosophieren müssen.
König Midas - alles was er anfasste wurde zu Gold
In der Quantenphysik wird diese 'In-Beziehung-Setzung' mit einem beobachtenden System als Dekohärenz (= wörtl.: aus dem Zusammenhang nehmen) bezeichnet wird. - Um etwas in Beziehung setzen zu können braucht man ganz einfach ein weiteres System, zu dem man Bezug nimmt. Leider wird diese einfache, selbstverständliche Voraussetzung in den Naturwissenschaften regelmäßig 'als so selbstverständlich' vorausgesetzt, dass sie keine, oder nur geringe Beachtung findet - und vergessen wird. (siehe auch "das Erkenntnisproblem in den Naturwissenschaften"). Wenn man aber in der Quantenphysik 'vergisst', dass 'das Bezug nehmende System' (= also das beobachtende System) - selbst ein Quantensystem ist und unauflöslich mit dem zu untersuchenden System in Zusammenhang steht, hat man ein Problem, wenn man das zu messende System "aus diesem Zusammenhang" nimmt und meint es so betrachten zu können!
Daher ist Dekohärenz nichts anderes als der Vorgang der die Verschränkung von beobachteten System, mit dem Beobachtersystem beschreibt und diese dadurch aus dem globalen Zusamenhang nimmt. Was passiert nun bei dieser "Verschränkung"?
Betrachten wir nun innerhalb der hier weiter oben erarbeiteten Abstraktion nochmal zwei vereinfacht dargestellte Quantensysteme.... kohärentes Quantensystem: Ein Quadrupol 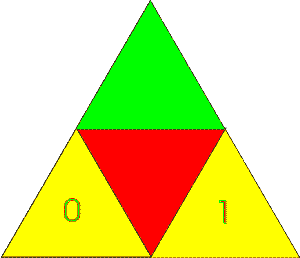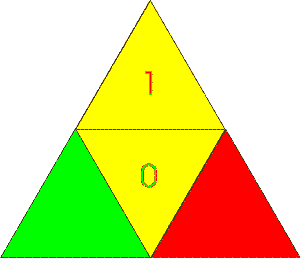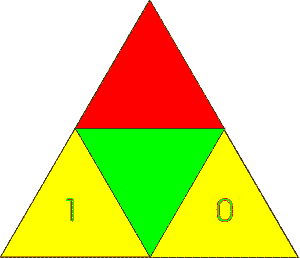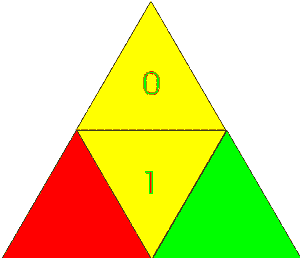 :Beobachter (Subjekt) - das zu Beobachtende (Objekt) ...., die wir miteinander verschränken wollen. Durch Beobachtungen hat man herausgefunden, dass sich Quantensysteme nur dann verschränken (dekohärieren), wenn diese orthogonal (= senkrecht) zueinander in Bezug gebracht werden. Das geschieht unter natürlichen Bedingungen laufend, wenn z.B. Photonen auf einen "Gegenstand" auftreffen oder von diesem absorbiert werden (und ist regelmäßig nicht, bzw. nur schwer zu verhindern). Setzt man nun diejenigen Eigenschaften des Quantensysteme orthogonal in Bezug, die zueinander gehören, erhält man folgendes Gesamtsystem mit dipolaren Eigenschaften: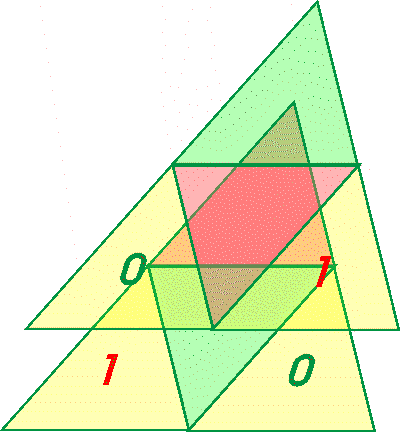 
=>
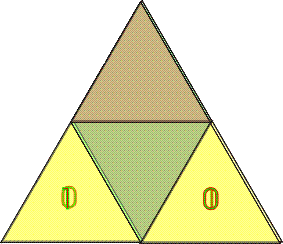 jeweils 2 senkrecht zueinander stehende Pole bilden eine Bühne, - damit 2 andere Pole reale Werte annehmen können
Subjekt und Objekt verschränkt = 1 verschränktes (dekohärentes) Quantensysteme Wie man nun erkennen kann, erscheint - für das verschränkte Quantensystem - die polare Information 1 oder 0 von der impliziten "Bühne der Realtiät" separiert. Und obwohl die Superpositin natürlich global weiterhin existiert, ist diese Information für die partial verschränkten Systeme nicht mehr greifbar. Sie sind dekohäriert. Noch etwas wichtiges ergibt sich hieraus: Die Verschränkung / Dekohärenz selbst stellt für das partielle System einen irreversiblen Speichervorgang dar! Was im folgenden eine wichtige Rolle spielen wird:
Da nun ein Beobachter zwischen den Entscheidungsmöglichkeiten 0 und 1 real, also 'in Wirklichkeit' (= partial verschränktes Quantensystem) wählen kann, haben wir damit eine 'physikalische Begründung' erhalten, warum "wir Quantensysteme" tatsächlich eine 'freie Wahl' haben! Und je nach dem was "ich" wähle (Ort oder Impuls) des beobachteten Quantensystems, ergeben sich verschiedene Möglichkeiten der Ausdifferenzierung innerhalb des nun uns gemeinsamen Systems.
Formbildung Ausdifferenzierung der Wirklichkeit Je nachdem welche Messung (Verschränkung) ich jetzt auf welcher Ebene zuerst durchführe, erhalte ich unterschiedliche Messergebnisse
zuerst: zuerst: (es kann aber je nachVerschränkung zu anderen Ergebissen kommen) Da diese "Formbildungen" (= Speichervorgänge) irreversibel sind, ergeben sich für partiellen Quantensysteme unterschiedliche Entwicklungswege im Multiversum
mögliche Entscheidungen
faktische (irreversible) Entscheidungen - in der selbstreflexiven Nachhersage Erfolgreiche Entscheidungen, - also Verschränkungen (= Speichervorgänge im Multiversum), die vom Ergebnis her für das beobachtende System in der "Nachhersage" einen sinnvollen Kontext eingehen, - werden von den verschränkten Quantensystemen selbstreflexiv ausgewählt.
Instantane Fernwirkung: Entscheidungen im Multiversum So entstehen - von einem Beobachter rückwirken betrachtet - 'Haupt-Entscheidungswege'. Es sind z.B. solche, die wir in der Schule als unverrückbare physikalische Naturgesetzte kennen gelernt haben. So dürften auch die (von Rupert Sheldrake) sogenannten "morphischen Felder, sich als ebensolche Entscheidungsgewohnheiten entpuppen, die sich schon mehr (wie z.B. Naturgesetze) oder weniger (z.B. neue chemische Verbindungen) stark ausgeprägt haben.
Gesetze der Biologie: Gene entscheiden sich für ihre eigene Vervielfältigung... Entlang dieser kaskadierenden Entscheidungsbäume errechnet sich ständig vor uns das, was wir als Wirklichkeit bezeichnen. Und diese Entscheidungen sind nicht an bewusste Wesen mit entsprechender Intelligenz gebunden, sondern sie gehören zu den natürlichen Eigenschaften eines jeden noch so rudimentären Quantensystems, - zur Grundeigenschaft von All_das_was_ist. Das was wir bislang für feste Materie ("Hardware") mit physikalischen Eigenschaften gehalten haben, entpuppt sich nun als aus abstrakter Information zusammensetzt, - und das was wir als flüchtig und immateriell (Software) befunden hatten, ist die wahre Eigenheit des Kosmos: Es gibt keinen Unterschied /Widerspruch zwischen Geist und Materie! Alles ist Eins wir (Quantensysteme) sind ALL_Ein
|
|
|
|
|
|
|
)
=
Qubits die ein einzelnes Photon zusammensetzen:
) Diese ist im wesentlichen von der
Masse des hineinfallenden Objektes (
MObj ) und des schwarzen Loches
( Msl
) abhängig.
= 
m) und bei einer Masse von 
Wasserstoffatomen. Das gesamte Universum in einem schwarzen Loch
konzentriert hätte dementsprechend eine Masse von 
kg..
Bit an unbekannter Information enthält.
Qubit! 
oder 
